Si una variable independiente x está creciendo indefinidamente através de valores positivos se escribe 
, y si decrece a través de valores negativos se denota como 
.
, y si decrece a través de valores negativos se denota como 
.
Similarmente cuando una funcion f(x) crece indefinidamente y toma valores positivos cada vez mayores, es escribe ƒ(x)→ + ∞ y si decrece tomando valores negativos se escribe ƒ(x)→ - ∞.
Infinito, la palabra aparece regularmente en los conceptos Matemáticos, esta es básicamente sólo una idea y no un número. Una cantidad extremadamente grande la cual no está definida puede ser considerada como infinito. Cuando se calcula el límite de una fracción, en la que el numerador se acerca a una cantidad positiva o negativa, si el denominador se mueve hacia 0, entonces en ese caso se dice que el límite es inexistente. Con el fin de explicar el comportamiento de tales funciones, decimos que
Esto indica que el límite de F® es un número desconocido de gran tamaño. Este tipo de límites es conocido como Límite Infinito. Los límites infinitos significan básicamente que el límite es imaginario, es decir, el valor de la función se puede hacer tan grande como queramos tomando los valores de r suficientemente cerca de 0.
Por ejemplo: una función x = 3y tiene límites infinitos. A medida que y aumenta, 3y también aumenta y cuando y se acerca al infinito, el límite de 3y se vuelve infinito.
Además la definición de límite infinito puede ser girada para un límite de un solo lado. El grafico correspondiente de la función g(x) =
que también posee límites infinitos puede ser dibujada como:
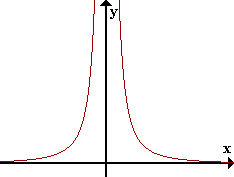
x −1 −0.1 −0.01 −0.001 0 g(x) 1 100 10,000 1,000,000 indefinido
Un concepto casi similar es el de “limites al infinito”. En este cuando la función de una variable y aumenta ilimitadamente entonces esta es mostrada como
. De manera similar, cuando y cae de manera ilimitada, entonces esta es mostrada como
.
El concepto principal de límites al infinito yace en dos puntos.
1). Cuando k es un número no negativo, entonces
2). Cuando k es un número no negativo, entonces
Encontrar el límite de un número racional al infinito es un caso especial en este concepto. Una regla sencilla para determinar el límite al infinito de tales números es considerando la variable, tanto en el numerador y en el denominador, que tenga el mayor exponente. Ahora bien, los límites pueden ser evaluados en base a las siguientes reglas:
1). Si el numerador con el más alto exponente va junto al denominador con el más alto exponente, en ese caso, el limite al infinito y el infinito negativo es la proporción de ambos coeficientes de mayor término.
2). Al dividir el numerador con el denominador, si el exponente resultante en la variable queda igual, en ese caso, el límite al infinito y el infinito negativo son infinitos. Si resulta impar, en ese caso, el límite al infinito es infinito y el infinito negativo es infinito negativo. Sin embargo, en ambas condiciones, el numerador debe tener el término más alto.
3). En la fracción impropia, es decir, en la cual el denominador contiene el término más alto, el límite al infinito y el infinito negativo es 0.
Los límites infinitos siguen unas propiedades importantes al infinito, las cuales son:
1).
disminuirá en una proporción igual y eventualmente llegará cerca de 0.
2). Del mismo modo, si r se convierte grandemente negativo, , se convertirá menos negativo y también se aproximará más a 0.
, se convertirá menos negativo y también se aproximará más a 0.
3). Además, un ejemplo similar ocurre cuando r es elevado a algún exponente, es decir,
