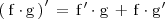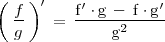Derivada una función constante
La derivada de una función constante es cero.
Ejemplo
Si  , entonces
, entonces
 , entonces
, entonces
Derivada de una suma de funciones
La derivada de la suma de dos funciones es igual a la suma de las derivadas de dichas funciones:
Este resultado, se puede ampliar a cualquier número de funciones:

Derivada de una diferencia de funciones
La derivada de la diferencia de dos funciones es igual a la diferencia de las derivadas de dichas funciones:
Ejemplo

Derivada de un producto de funciones
Ejemplo

Observese que  y que la derivada de
y que la derivada de  es precisamente
es precisamente  .
.
 y que la derivada de
y que la derivada de  es precisamente
es precisamente  .
.Derivada de un cociente de funciones
La derivada del cociente  viene dada por la fórmula:
viene dada por la fórmula:
 viene dada por la fórmula:
viene dada por la fórmula:Ejemplo


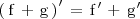
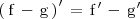
 y
y 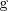 , viene dada por la fórmula:
, viene dada por la fórmula: